Bemærk, at der til alle tider kan skiftes mellem kalkulationsmetode, også uden at der går data tabt.

 

Indtastning i indholdssiden

 

Ved successiv kalkulation kan mængde og enhedspris cellerne deles op i 3: minimum, typisk og maksimum celler. Læs mere om hvordan de tilhørende kolonner slås til og fra.

 

Mgn Min	Minimum mængde for komponenten.
Mgn Typ	Typisk mængde for komponenten.
Mgn Max	Maksimum mængde for komponenten.
EP Min	Minimum enhedspris for komponenten.
EP Typ	Typisk enhedspris for komponenten.
EP Max	Maksimum enhedspris for komponenten.
Std. afv.	Standard afvigelse for den samlede kostpris.
Prioritet	Prioritetstal for komponentens underpunkter, der ligger mellem 0 og 100. Størrelsen af prioriteten beskriver hvor der er størst spredning i kostprisen.

 

Generelt om successiv kalkulation i Sigma 2010

 

Sigma 2010 anvender principperne beskrevet i bogen "Projekt planlægning - i en foranderlig verden" af Steen Lichtenberg, med følgende formler til udregning af hhv. standardafvigelser

Standardafvigelse, mængde = (max. mængde – min. mængde) / 4,6
Standardafvigelse, enhedspris = (max. enhedspris – min. enhedspris) / 4,6

-samt sandsynlige værdier (middelværdier):

Sandsynlig mængde = (min. mængde + 2,9 * typ. mængde + max. mængde) / 4,9
Sandsynlig enhedspris = (min. enhedspris + 2,9 * typ. enhedspris + max. enhedspris) / 4,9
Sandsynlig pris = sandsynlig mængde * sandsynlig enhedspris

 

Beregning af standardafvigelse for linjer uden underkomponenter

 

For linjer uden underkomponenter, udregnes standardafvigelsen for linjen som;

Standardafvigelse, linje = KVADRATROD((std.afv., mængde * sand. enhedspris)^2 + (std.afv., enhedspris * sand. mængde)^2)

 

Beregning af standardafvigelse for linjer med underkomponenter

 

Først beregnes følgende hjælpetal (som er den samlede std. afvigelse af underkomponenterne).

Standardafvigelse, underkomponent = KVADRATROD(std.afv., underkomp.1^2 + std.afv., underkomp.2^2 + …)

 

Desuden bemærkes:

Sandsynlig underkomponent pris = summen af de sandsynlige priser på alle underkomponenter.

Herefter kan standardafvigelsen for linjen med underkomponenter udregnes således:

std.afv., linje = KVADRATROD((std. afv., mængde * sand. underkomponent pris)^2 + (std.afv., underkomp. * sand. mængde)^2)

 

Eksempel

 

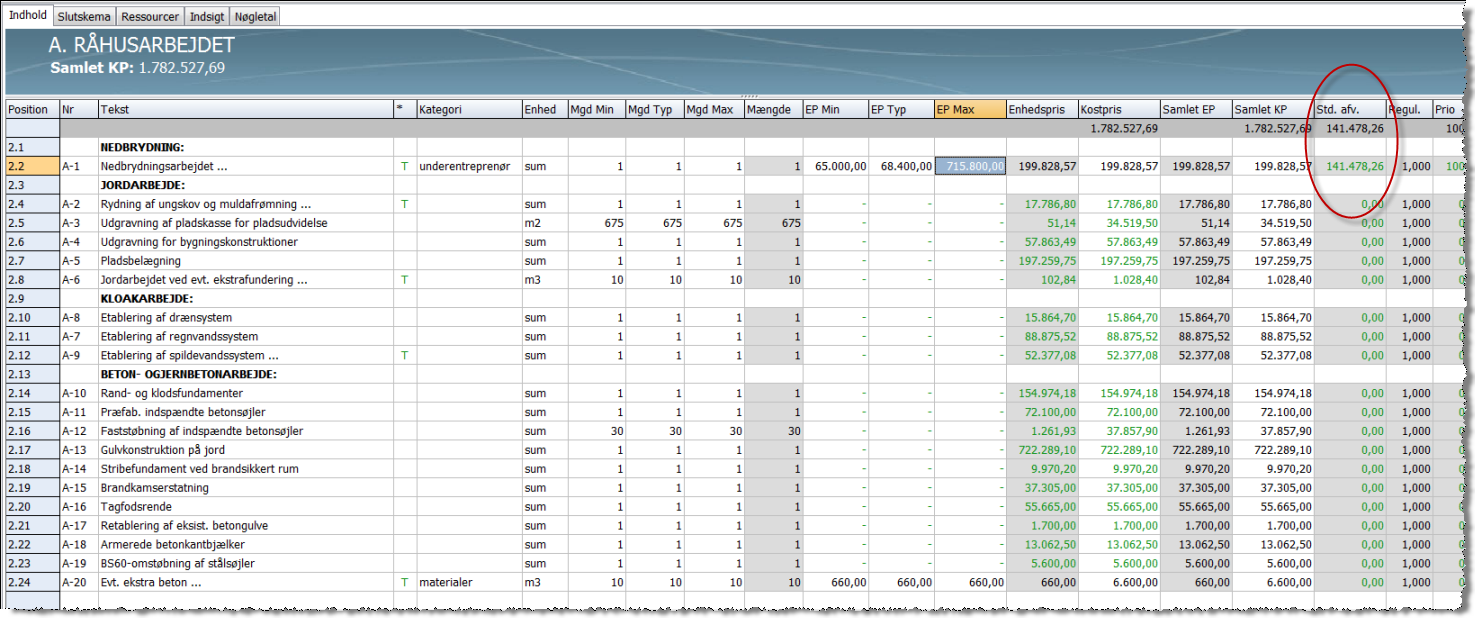
Følgende viser kalkulationen, der anvendes som eksempel på beregning af en successiv kalkulation ved brug af Sigma 2010 

 

 

Som det ses, er kalkulationen bygget op af 3 hovedoverskrifter, hvoraf den sidste består af en komponent med underkomponenter.

 

Beregning af "1. Byggeplads" og "2. Jordarbejde"

Eftersom disse 2 hovedoverskrifter hver især blot består af en enkelt komponent (uden underkomponenter), kan disse regnes ud som følger:

 

	1.1	2.1
stdMængde = (maxMængde – minMængde) / 4,6	(8-6)/4,6 = 0,6522	(150-110)/4,6=8,6957
stdEnhPris = (maxEnhPris – minEnhPris) / 4,6	(1200-950)/4,6 = 54,3478	(90-50)/4,6=8,6957
sandMængde = (minMængde + 2,9*typMængde + maxMængde ) / 4,9	(5 + 2,9*6 + 8) / 4,9 = 6,2041	(110 + 2,9*120 + 150) / 4,9 = 124,0816
sandEnhPris = (minEnhPris + 2,9*typEnhPris + maxEnhPris ) / 4,9	(950 + 2,9*1000 + 1200) / 4,9 = 1030,6122	(50 + 2,9*60 + 90) / 4,9 = 64,0816
sandPris = sandMængde * sandEnhPris	6,2041 * 1030,6122 = 6394,0025	124,0816 * 64,0816 = 7951,3536
stdLinje = KVADRATROD((stdMængde*sandEnhPris)^2 + (stdEnhPris*sandMængde)^2)	KVADRATROD((0,6522*1030,6122)^2+(54,3478*6,2041)^2) = 751,9703	KVADRATROD((8,6957*64,0816)^2+(8,6957*124,0816)^2) = 1214,3660

 

Beregning af "3. Betonarbejder"

Denne hovedoverskrift består af en komponent (3.1 Fundamenter), der har 2 underkomponenter (3.1.1 og 3.1.2). For position 3.1 kender vi kun mængderne, hvorimod prisen beregnes successivt for underkomponenterne.

Først beregnes standardafvigelse samt sandsynlig mængde for position 3.1:

 

	3.1
stdMængde = (maxMængde – minMængde) / 4,6	(180-120)/4,6 = 13,04348
sandMængde = (minMængde + 2,9*typMængde + maxMængde ) / 4,9	(120 + 2,9*140 + 180) / 4,9 = 144,0816

 

Eftersom komponent 3.1 består af to underkomponenter (3.1.1 og 3.1.2), er det nødvendigt først at beregne standardafvigelsen for underkomponenterne, før vi kan beregne position 3.1. Idet komponenterne 3.1.1 og 3.1.2 ikke selv har underkomponenter, foretages beregningen på samme måde som ovenfor.

 

	3.1.1	3.1.2
stdMængde = (maxMængde – minMængde) / 4,6	(1,1-0,8)/4,6 = 0,06517	(1,5-0,8)/4,6 = 0,152174
stdEnhPris = (maxEnhPris – minEnhPris) / 4,6	(155-100)/4,6 = 11,95652	(240-180)/4,6 = 13,04348
sandMængde = (minMængde + 2,9*typMængde + maxMængde ) / 4,9	(0,8 + 2,9*0,95 + 1,1) / 4,9 = 0,95	(0,8 + 2,9*1 + 1,5) / 4,9 = 1,0612
sandEnhPris = (minEnhPris + 2,9*typEnhPris + maxEnhPris ) / 4,9	(100 + 2,9*120 + 155) / 4,9 = 1030,6122	(180 + 2,9*195 + 240) / 4,9 = 201,1224
sandPris = sandMængde * sandEnhPris	0,95 * 1030,6122 = 116,9082	1,0612 * 201,1224 = 213,4361
stdLinje = KVADRATROD((stdMængde*sandEnhPris)^2 + (stdEnhPris*sandMængde)^2)	KVADRATROD((0,06517*116,9082)^2+(11,95652*0,95)^2) = 13,908	KVADRATROD((0,152174*201,1224)^2+(13,04348*1,0612)^2) = 33,59025

 

Herefter beregnes den samlede standardafvigelse for underkomponenterne:

stdUnderkomp = KVADRATROD(stdUnderkomp1^2 + stdUnderkomp2^2 + …) = KVADATROD(13,908^2 + 33,59025^2) = 36,3557

 

Samt summen af de sandsynlige priser for underkomponenterne:

sandUnderkompPris = summen af de sandsynlige priser på alle underkomponenter = 116,9082 + 213,4361 = 330,3442

 

Til sidst er det så muligt at beregne standardafvigelsen for komponent "3.1 Fundamenter":

stdLinje = KVADRATROD(  (stdMængde * sandUnderkompPris)^2 + (stdUnderkomp * sandMængde)^2 )
= KVADRATROD( (13,04348 * 330,3442)^2 + (36,3557 * 144,0816)^2) = 6782,677

 

Beregning af standardafvigelse for den samlede kalkulation

Vi har hermed følgende standardafvigelser for de 3 hovedoverskrifter:

 

1. Byggeplads	751,9703
2. Jordarbejde	1214,3660
3. Betonarbejder	6782,677

 

Standardafvigelsen for den samlede kalkulation fås så ved;

stdUnderkomp = KVADRATROD(stdUnderkomp1^2 + stdUnderkomp2^2 + …) = KVADRATROD(751,9703^2 + 1214,3660^2 + 6782,677^2) = 6931,439

Hvilket også stemmer overens med det resultat som Sigma 2010 har beregnet (når der tages hensyn til afrundingsdifferencer i forhold til Excel):

 

 

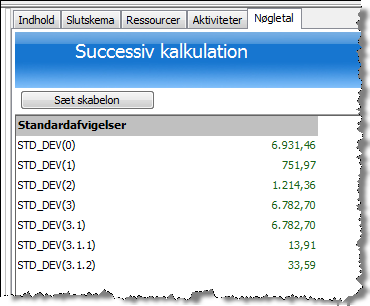
Brug af nøgletalsfunktioner til at finde standardafvigelse

 

Sigma 2010 indeholder en nøgletalsfunktion (STD_DEV), der kan anvendes til at finde standardafvigelsen på for en given position i kalkulationen.

I følgende eksempel er vist hvorledes denne funktion er anvendt i nøgletalsskemaet på vores kalkulation:

 

See Also